A Mathematician's Lament and the Core Issues with Modern Education

https://www.maa.org/external_archive/devlin/LockhartsLament.pdf

This is one of the most important essays on education I've read in a long time. Someone was kind enough to make a video of it if you prefer to watch:

I remember thinking that I must be incredibly dumb because I simply did not understand math. I knew that the fault had to lay with me because I knew that I had phenomenal teachers all my life.

I didn't question why I had to learn these concepts I just knew that they were important and I didn't understand how to operate them properly.

I understood my English classes and while I didn't do well overall I knew that my poor performance in my humanities classes stemmed from not doing my homework and not writing well as opposed to not understanding the content.

Paul Lockhart suggests that the problem is that very few people can possibly learn math well given how it is taught. Math is taught poorly because the purpose of math is not understood. His analogy of denying kids access to the practice of art in favor of the theory of art is perfect; I would absolutely hate drawing if I had to master art theory before I tried to sketch. That is effectively what we are doing when it comes to math education. Honestly that is what we are doing with most subjects - favoring the scalable theory at the cost of the harder to teach, but infinitely more valuable, practice.

We do this with science - I see some of my brilliant chemistry students who have figured out how to balance equations and solve calorimetry problems but who have never lit up a Bunsen burner in their middle school science class or grown a salt crystal in the lab. Or the academically gifted kid who took the AP biology exam in ninth grade but only watched lab videos the entire year. By focusing on the easily disseminated content we deny the kids the chance to actually apply any knowledge. For some reason we do that and tell them that someday they will need to know this information for some future career.

But the purpose of math isn't for a career. The purpose of math isn't for future discoveries. The purpose of math is to appreciate the beauty of the universe and to express that beauty in ways that are universally true. This is true of the purpose of poetry, art and literature. We don't need these things to get us a job - we need these things because they are part of the creative impulse which separates us from the almost all the other species on earth.

Lockhart argues, for example, that the purpose of Algebra isn't for figuring out compound interest, something practical, or for solving X, something man made. The purpose of algebra is to demonstrate and express the universal beauty of symmetry.

This is a concept that can be intuitively understood with a see-saw. If a child weighing 75 pounds gets on one side of the see-saw there are multiple ways that the see saw can balance - with another kid the same weight or multiple kids whose summed weight equal the child. We can also balance the see-saw with a heavier person who only uses some portion of their weight on the other side, as an adult who might balance their weight using their feet. This fundamental truth is expressed mathematically in Algebra along with other ideas.

Lockhart thinks of math as a kind of exploratory play. He suggests that kids should spend their time intuitively grasping mathematical principles through playing games like Chess and Go - there are intuitive principles at work in these games that can help kids grasp math concepts.

Later, Lockhart suggests a kind of dialogue between teacher and student to help students find the math concepts that matter on their own.

Geometry was a form of torture back in 1992 when I was fourteen. It was only when I started to learn how to draw that I started to discover the joys that can be found in geometry. Drawing helped me to develop greater interest in geometry. I think that the main issue for me was the formal nature of proofs. When I ask students why they hate geometry they universally tell me that proofs are what they hate. The formality of it and the abstract nature of proofs is the bane of every high school freshmen.

I think they also hate the fact that they don't ever see proofs again in math. They work hard for a year on learning to regurgitate the proofs but when they take trigonometry the following year they are not required to continue to develop the rigorous logic of proofs in trig.

But what if we taught geometry less through the lens of abstract logic and more through the lens of drawing and exploring the relationships between fundamental shapes?

Asking students to figure out the relationship between squares and triangles and show the relationship through drawing.

By asking students to make as many other shapes as possible with triangles they can begin to understand concepts like why the area of a triangle is equal to 1/2 the base of the triangle times the height.

This is something that students can independently derive! Rather than just feeding students the algorithm they can figure this out and express it in their way.

Start with a relatively simple discovery like this and then ask students to make other shapes out of triangles. The opportunity for creativity, beauty and joy becomes tremendous!

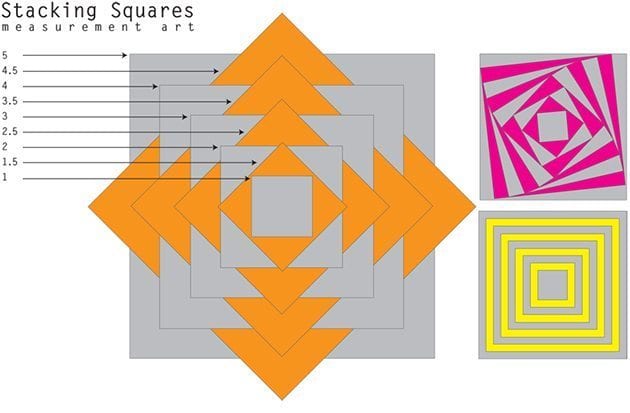
As students become more confident in their ability to explore the relationships between shapes they can develop more and more sophisticated constructions. Exploring the relationship between lines and circles offers another opportunity to engage in wonder.

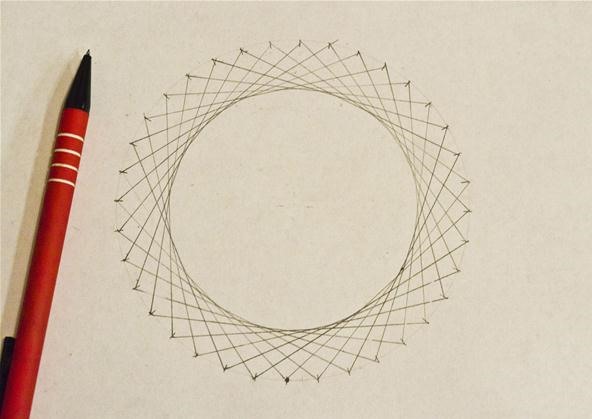
Students who are taught how to construct a circle out of straight lines can start to intuit the rules for circumference, diameter and radius.

But in order to internalize the abstract they need to engage in the drawing and construction of shapes. In other words they need to work with their hands in order for their minds to grasp the abstract concepts.

But our education system has come to primarily prize abstract analysis. There is nothing inherently wrong with abstract analysis but very few people are willing to take the tremendous amount of time it takes to grasp concepts at this level. The kids that we label as being "intelligent" are mostly the kids who can correctly demonstrate their ability to regurgitate abstract analysis and plug values into a designated algorithm and return the correct value. The kids that don't do this well become the "artistic" kids or the "physical" kids.

I have a tremendous amount of respect for elementary school teachers. I struggle to imagine what it takes to get a kid to jump the chasm between "not being able to read" and "read" - I don't know if I have the temperament to work with kids through the stumbling that is inevitably going to happen through that process. And honestly I am in awe of good middle school teachers. The ability to work with kids in the beginning of puberty and the journey of adolescence requires a tremendous amount of patience, joy and imagination to reach them. But we seem to lose this joy and imagination when students reach middle school in favor of delivering algorithms and rote problems.

The main reasons we prize abstract analysis is that it can be delivered at scale and it requires concentration and discipline to achieve; two values that are highly valued in most white collar work.

Maximizing the abstract analytical comes at a cost; we give enormous short shrift to the creative and exploratory.

I share Lockhart's lament. I see in biology how our state exams think of biology almost exclusively in terms of genetics and sub-cellular research. You would think that all of life can be described as the movement of biochemicals and energy based on the subject breakdown of the AP biology exam.

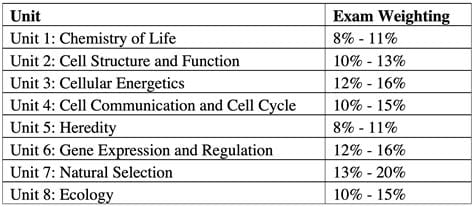
There is next to nothing on the exam about human body; the part that most kids are understandably the most interested in exploring. There is nothing on this exam about animals; the subject that draws most peoples interest in biology when they are kids. With the exception of the equation on photosynthesis and some abstract concepts in ecology about primary producers there is nothing about plant life. There is no phenomena that can be personally observed or explored - just abstractions that can be marked on paper. The only thing that seems to matter is abstract analysis of things that students can't see.

I think if you could start teaching subject matter to kids from a young age in a creative way, and continued down that path for their entire primary and secondary education career, then you could probably see a lot more kids loving the subjects that they typically find the most stressful. Part of why humanities are typically more loved in school is because imagination, beauty and joy are more accessible; a good book invites these values of human expressions in a way that a textbook or problem set don't allow.

I don't know if creative exploration of subject matter can be scaled. Our need to categorize by level of excellence, coupled with our human desire to signal out to the world our excellence, is achieved much easier with grades than with general feedback on work.

Abstract analysis, which is what we prize in education, is easily scaled. Our ability to correctly answer multiple choice questions is easily scalable. Unfortunately maybe 10-20% of students wind up getting anything out of classes that are highly abstract in nature. Most of the students that do get a good grade in those classes are those students that have learned how to memorize information for a test. A tiny number of those students ever wind up valuing the information beyond its ability to offer a good grade.

I am generally against coercive education. I don't like the fact that kids need to take a certain number of years of math, language and science education. Mandating students learn specific domains of knowledge stunts emotional development. The mandatory system of education turns school into a contest of signals whereby we reward the student with the best grades with the shiny reward of the next step up - the fancy college or the prestigious job. We could get rid of this idea of a minimum number of years if we could make the learning so good that students would want to continue to learn. I would be much happier if we could ensure that every kid was competent in basic arithmetic and fluent with fractions, decimals and the basic principles of finance and accounting. If people want to explore math beyond this level they are welcome to it.

Ideally you convince people that something is worth their time and effort. If you can't do that then don't force them to learn it "for their own good".

Nothing tamps down the human impulse to create more than a grade. Grades tell students "focus on making someone else, the teacher (or the parents) happy" instead of "focus on the joy of the discovery process".

Human beings are creative creatures. I see it in my four year old; his very impulse is to look at objects in the house and see their potential to be combined into art. We encourage that impulse for a little while but bit by bit we eliminate that kind of creative exploration in learning until it is only left in the "artistic" classes.

Those of us who continue to pursuing learning for the joy of it after we finish school rediscover the joy that we had when we were young. Unfortunately 90% of people decide that they are done with the joy of learning after they finish their required academic journey. It doesn't have to be this way.

I spend about ten hours a week thinking and honing my writing into a ten minute read. If you find my work interesting or valuable I'd love it if you shared the link with anyone you think might enjoy reading my essays.